2. Aborder la quête spirituelle en suivant une démarche scientifique ?

Même ce qui semble le plus concret, rationnel et indiscutable, comme les mathématiques, repose sur des hypothèses. En effet, les énoncés démontrés sont toujours de la forme : si on suppose XX, alors on peut prouver YY en utilisant un raisonnement (même si parfois les hypothèses XX ne sont pas explicitement formulées). Les hypothèses de base sont appelées axiomes. Définition du Larousse pour ‘Axiome’:

• Dans la logique aristotélicienne, point de départ d’un raisonnement considéré comme non démontrable, évident.
• Énoncé initial d’une théorie axiomatisée, qui sert de point de départ aux démonstrations dans cette théorie.
• Énoncé indiscuté, admis comme base d’une construction intellectuelle, sociale, morale, etc.; vérité admise par tous sans discussion.

Par exemple, la géométrie dans le plan (par exemple, sur une feuille de papier) vue par Euclide repose sur les 5 axiomes (aussi appelés postulats) suivants, appelés Axiomes d’Euclide ( www.bibmath.net):

1. il existe toujours une droite qui passe par deux points du plan.
2. tout segment peut être étendu suivant sa direction en une droite (infinie).
3. à partir d’un segment, il existe un cercle dont le centre est un des points du segment et dont le rayon est la longueur du segment.
4. tous les angles droits sont égaux entre eux.
5. étant donné un point et une droite ne passant pas par ce point, il existe une seule droite passant par ce point et parallèle à la première (l’axiome des parallèles).

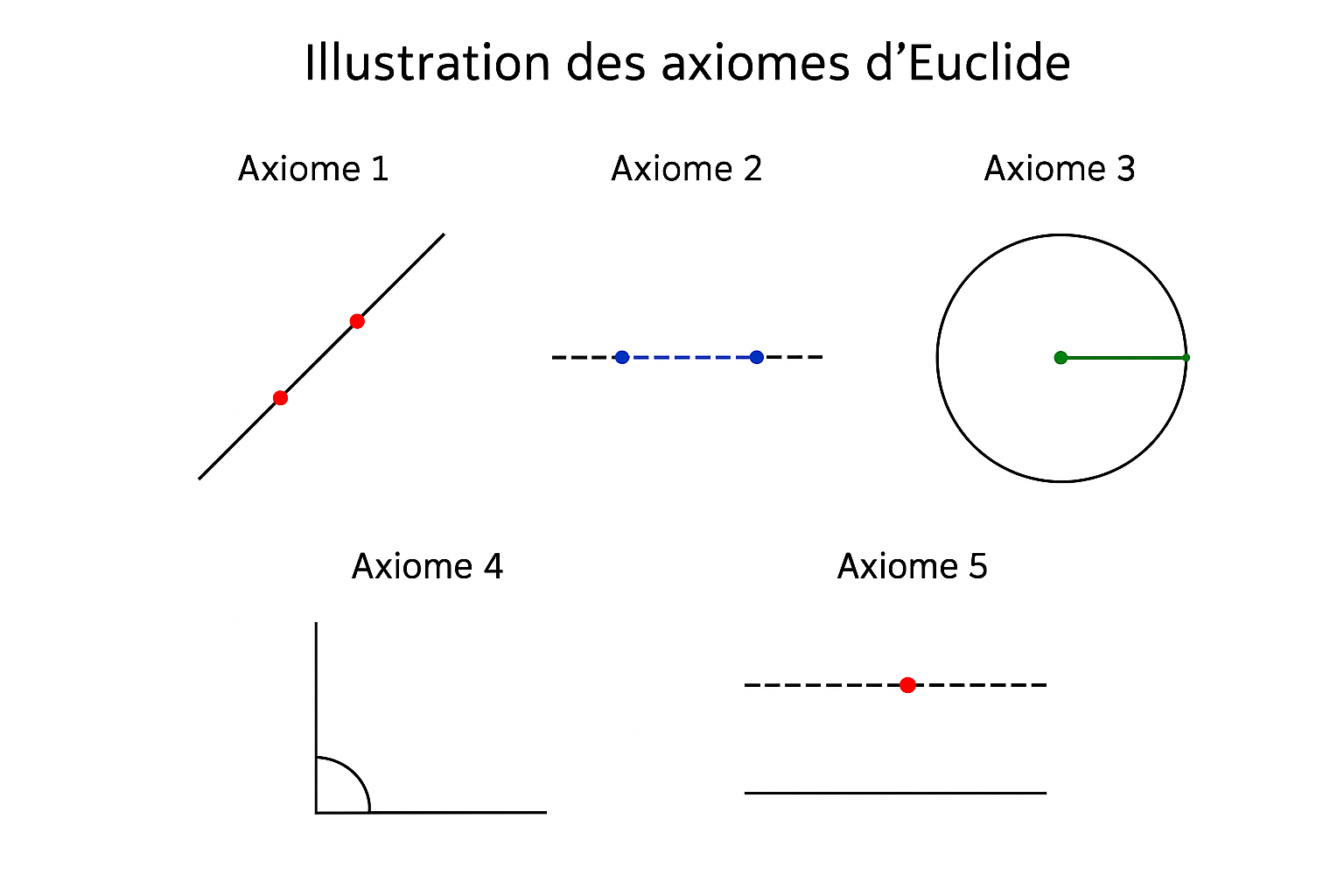
Ces affirmations sont faciles à vérifier par l’expérience. En effet, lorsqu’on dessine deux points sur une feuille de papier, il est aisé de tracer une ligne entre eux à l’aide d’une règle. Cependant, il est impossible de les démontrer formellement. En se basant sur ces axiomes, il est possible de déduire et démontrer le reste des propriétés de la géométrie dans le plan. Par exemple, en se basant sur l’axiome des parallèles, on peut démontrer que la somme des angles d’un triangle est égale à 180 degrés.

Il en ressort que rien n’est totalement démontrable, pas même les mathématiques, qui reposent elles aussi sur des hypothèses, qu’elles soient explicites ou implicites. En somme, tout est relatif. Les sciences telles que la physique, la cosmologie, la biologie et même la médecine ne font pas exception.

En effet, lorsqu’on réalise un essai clinique et qu’on montre qu’un médicament est plus efficace qu’un placebo, on s’appuie sur des outils statistiques. Mais même dans ce cadre rigoureux, il y a toujours une marge d’erreur. Par exemple, un seuil de signification statistique souvent utilisé est p < 0,05 — ce qui signifie qu’il y a 5 % de probabilité que le résultat observé soit dû au hasard, c’est-à-dire que l’on observe un effet positif sur les patients qui ont pris le médicament alors qu’en réalité, le médicament n’est pas plus efficace que le placebo. Mais au-delà de cette marge d’erreur, l’interprétation des résultats repose aussi sur plusieurs hypothèses sous-jacentes :

• Que les participants choisis représentent bien la population générale.
• Que les mesures utilisées (par exemple, les scores de symptômes) sont valides et fiables.
• Que l’effet observé est réellement dû au médicament et non à des biais non contrôlés (comme un effet d’attente, des erreurs de mesure, des facteurs contextuels).
• Que les analyses statistiques choisies sont appropriées pour les données.

Autrement dit, même un résultat « significatif » n’est jamais une preuve absolue. C’est une conclusion probabiliste, qui doit être interprétée dans un cadre méthodologique bien construit.

De plus, toute théorie scientifique telle que celle sur les atomes ou les lois de la gravité, vise à expliquer au mieux nos observations et repose également sur des hypothèses. Ces théories possèdent souvent des limites et évoluent avec les nouvelles découvertes.

Ce n’est pas parce qu’il y a des éléments qui ne semblent pas en accord avec une théorie ou semblent même la contredire dans certaines situations que cette théorie est entièrement fausse. Cela signifie simplement qu’elle n’est pas capable de tout expliquer. Elle est limitée, comme nous.

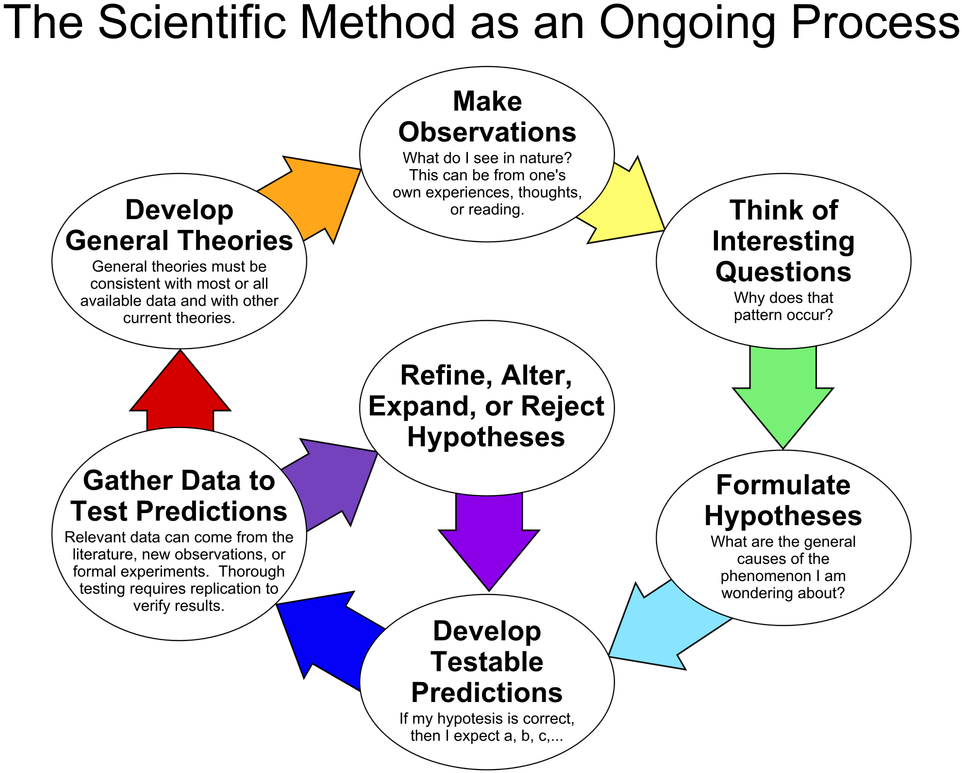
La démarche scientifique se compose de plusieurs étapes:

• Observer le phénomène: Que se passe-t-il dans la nature ? L’observation peut provenir de l’expérience, de la réflexion ou de recherches.
• Se poser des questions pertinentes: Pourquoi ce phénomène se produit-il ? Quels sont les facteurs qui l’influencent ?
• Formuler une théorie (et ses hypothèses/axiomes) pour décrire/expliquer le phénomène
• Faire des prédictions vérifiables: Si ma théorie est correcte, alors je devrais observer X, Y, Z…
• Expérimenter et recueillir des données:
  • Les données peuvent provenir d’études, d’observations ou d’expériences formelles.
  • Pour être valide, un test doit être reproductible.
• Analyser les résultats et ajuster la théorie si nécessaire.
  • Les résultats confirment-ils l’hypothèse ou faut-il la modifier ?
• Élaborer une théorie générale: Une théorie scientifique doit être cohérente avec la majorité des données disponibles et compatible avec d’autres théories existantes.

   

Dans ce blog, je vous propose d’aborder la quête de l’existence de Dieu en suivant une démarche inspirée de la méthode scientifique. L’objectif n’est pas de démontrer scientifiquement l’existence de Dieu — ce qui est impossible, puisque Dieu ne constitue pas un phénomène physique, mesurable ou directement observable. En revanche, si Dieu existe, il est légitime de s’interroger sur les effets que son existence pourrait produire sur le monde.

C’est dans ce sens que cette réflexion sera menée : en collectant des informations issues de différentes sources, en examinant quelles hypothèses permettent d’expliquer le plus grand nombre d’éléments observables, et en identifiant celles qui apparaissent les plus cohérentes, rationnelles et raisonnables.

Comme en science ou en mathématiques, cette démarche repose sur certains principes de départ intuitivement sensés — comparables aux axiomes d’Euclide en géométrie — qui ne peuvent être démontrés en eux-mêmes, mais à partir desquels il devient possible de construire une compréhension du réel et d’en tirer des conclusions.

Je vous propose ainsi d’examiner les différentes évidences, de formuler ces hypothèses de base, puis d’en explorer les implications. Cette réflexion demeurera ouverte : elle pourra évoluer à la lumière de nouvelles expériences, découvertes ou informations, tout comme c’est le cas dans la recherche scientifique.